
低歪な正弦波をどのように発生させるのが良いかを検討しているときに状態変数型発振回路というオペアンプを用いた発振回路の存在を知りました。低歪な発振回路としてウィーンブリッジ発振回路が紹介されている例は良く見かけます。しかし、状態変数型発振回路を製作している例は少ないようなので、実際に制作し、その特性を簡単に評価してみました。
DDSなどのデジタル的要素を使わずに正弦波を作るというのはロマンがあるのです!
状態変数型発振回路とは
状態変数型発振回路は、RC発振器の一種で、状態変数型フィルタ(ステートバリアブル型フィルタとも呼ばれている)というQ値の大きなフィルタを応用した形式です。
この発振回路は、初段のオペアンプの後段に積分回路が二段直列に接続された構成になっています。積分回路は、カットオフ周波数を境目にして-6dB/oct(-20dB/dec)で減衰する特性を持ちます。したがって、状態変数型発振回路の正弦波出力は、積分回路(LPF)によって高調波成分がカットされるため歪が小さくなります。
また、積分回路の1段目と二段目には90度の位相差が発生するため、正弦波と余弦波を取り出す2相発振器として用いることもできます。
回路構成
状態変数型発振回路の最終的な回路構成と各素子の定数は以下のようになりました。また、各半導体素子(IC1,IC2,IC3,IC4)へ供給する電源電圧は±12Vとして設計を行いました。
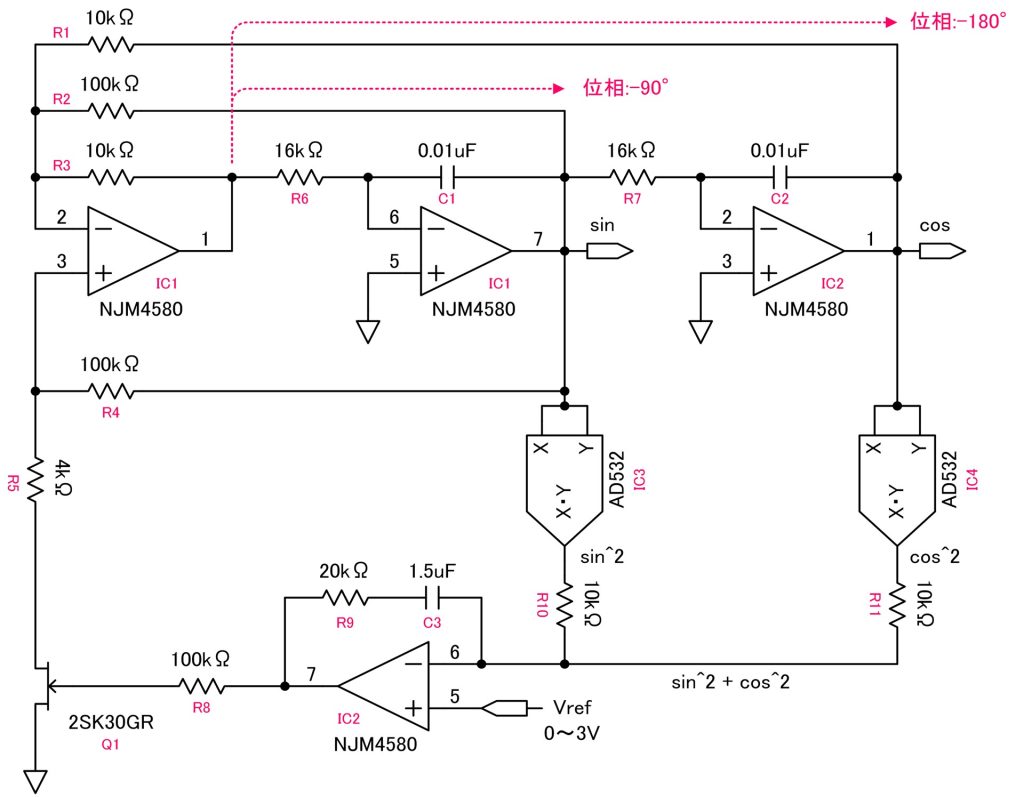
発振周波数
発振周波数は回路中のRC(C1,C2,R6,R7)を変更することによって設定します。今回の発振回路では発振周波数が1[kHz]となるように抵抗とコンデンサの値を決定してあります。
C=C1=C2,R=R6=R7とすると、発振周波数[Hz]は以下の式で求めることができます。
$$f=\frac{1}{2\pi\sqrt{C_{1}C_{2}R_{6}R_{7}}}=\frac{1}{2\pi{CR}}$$
製作した発振回路はC1=C2=0.01[uF],R6=R7=16[kΩ]としました。したがって、設計上の発振周波数は994.7[kHz]となります。
振幅制御回路(AGC回路)
振幅制御回路は、状態変数型発振回路の出力レベルを一定に制御するために必要です。この回路がない場合、回路の系には正帰還のループのみ存在することとなり、出力波形の振幅は電源電圧のレールに張り付いてしまいます(オペアンプが出力できる最大のレベルが出力されてしまう)。このため、オペアンプが出力できる電圧範囲に収まるように発振回路のゲインを制御する回路が必要です。
試しに、上記の回路構成で振幅を制御しているJFET 2SK30(Q1)のドレイン-ソース間を短絡してみます。すると、発振回路の出力はオペアンプの電源レール付近まで上昇し、正弦波のピーク付近がクリップして波形が歪んでしまうことがわかります。
振幅制御回路の基本構成
発振回路の出力振幅制御には、いわゆるフィードバック制御を用います。以下の図は発振回路の振幅制御系のブロック線図を表しています。制御対象となる発振回路(今回は状態変数型発振回路)、補償器、整流回路から構成されています。
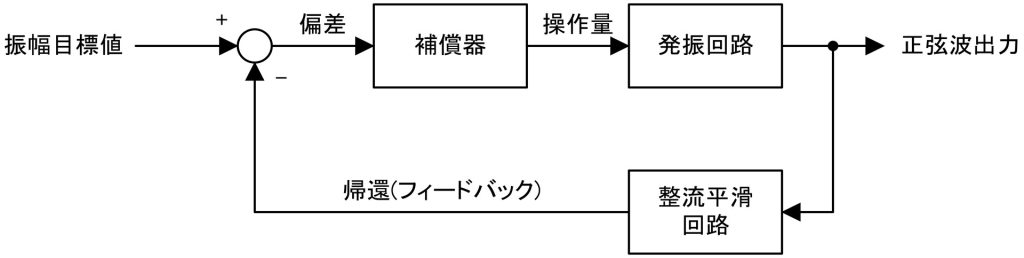
一般的に発振回路のフィードバック制御系は、基準電圧としてDC電圧を与える仕様になっていることが多いです。しかし、発振回路の出力はAC電圧(正弦波)なので、そのまま基準電圧と比較して偏差を得るということができません。そこで、発振回路の出力を整流平滑回路に通してDC電圧値としてから基準電圧との偏差を取得する必要があります。
整流回路
”出力に対して半波整流・全波整流を行い振幅レベルの絶対値を得る”という方式の回路がアナログ発振回路の振幅調整回路として良く紹介されているかと思います。これらの回路は、オペアンプとダイオードを用いた整流回路により発振回路の出力波形を整流(絶対値取得)し、後段のLPFにより平均値を得るというものです(いわゆる平均値整流方式)。
LPFのカットオフ周波数が十分に低域であれば、リップルの影響が小さくなり、実使用上は問題ないレベルになります。しかし、この回路では原理的にリップルを0にすることはできません。出力のリップルは高調波成分を含むため生成する出力波形の歪を引き起こす要因となります。
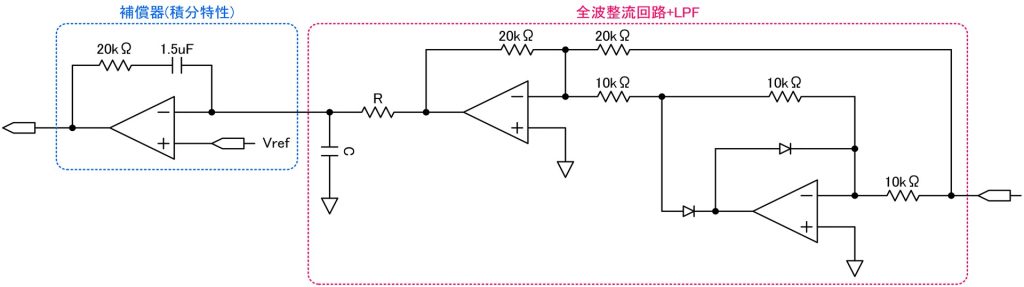
今回は、できるだけ低歪な発振回路を構築することが目標なので整流回路もリップルが小さいものを採用したいところです。そこで乗算器AD523を利用した理想的な整流回路を構築しました。積分回路の1段目と二段目には90度の位相差が発生するため、この出力を2つの乗算器に入力して加算すれば、理論的にリップルのないDC電圧が得られるという仕組みになっています。状態変数型発振回路の出力が90度位相差のある、2出力であることをうまく利用しています。
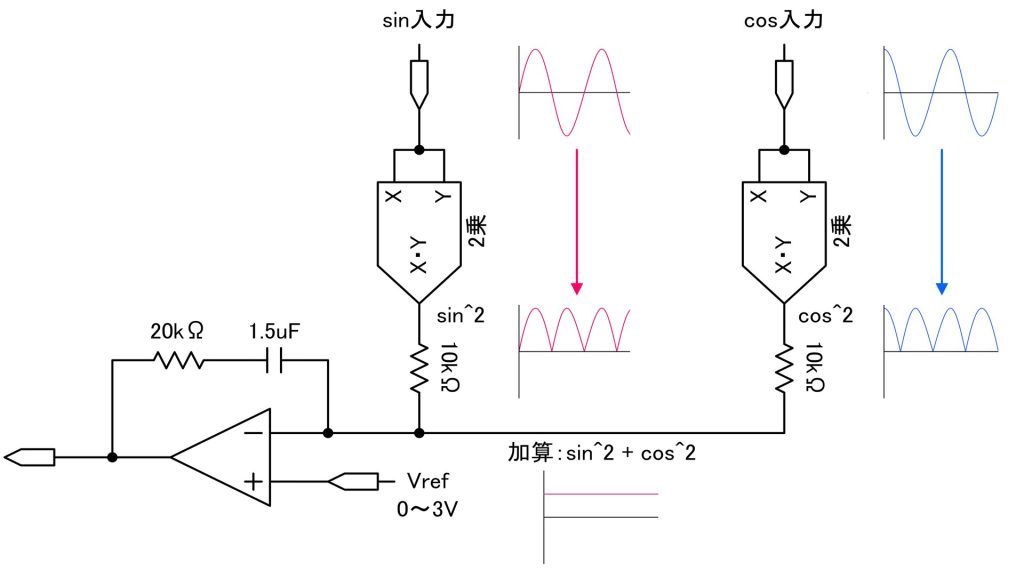
AD523という乗算器を使って理想整流回路を構成しています。秋月電子で入手できるAD633とほぼ特性が同じなので代用可能だと思います。
https://akizukidenshi.com/catalog/g/gI-13626/
製作した回路
発振回路は秋月電子のBタイプ基板上に実装しました。


基板にエッジマウントするタイプのSMAコネクタ便利ですね。片面基板でも、しっかりと固定できて良いです。
特性評価

動作確認
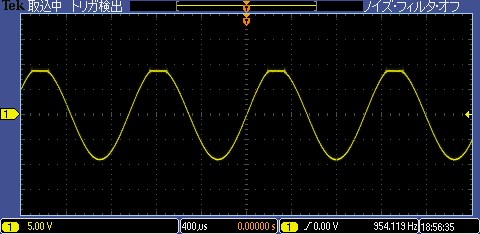
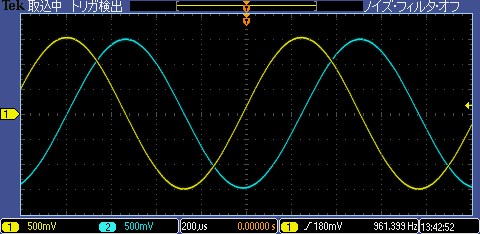
発振回路の振幅が1.5[Vp]となるように基準電圧を設定しました。この状態で発振回路の2相の出力をオシロスコープでモニタして観測しました。黄(1ch)と青(2ch)には90度の位相差があり、sin-cosの2相発振回路となっていることが確認できました。
黄(1ch):積分回路2段目の出力
青(2ch):積分回路1段目の出力
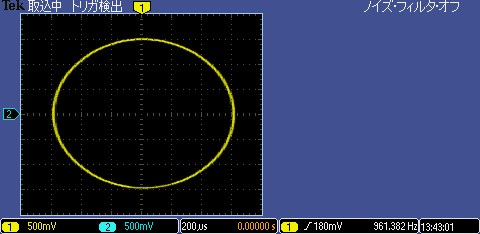
発振周波数は約961[Hz]となりました。設計値から約-3%の誤差があることになります。これは、抵抗器とコンデンサの定数誤差の影響が大きいと考えられます。抵抗器は許容差±1%を使用していますが、コンデンサについては許容差±10%品を使用しています。したがって、コンデンサの定数誤差による発振周波数への影響が大きいのではないかと考えています。
高調波の測定
発振回路の振幅が0.8[Vp]となるように基準電圧を設定しました(ADP3250の1Vレンジを用いるため)。この状態で発振回路の出力をADP3250に入力し、FFT解析を行うことで出力信号に含まれる高調波成分を測定します。
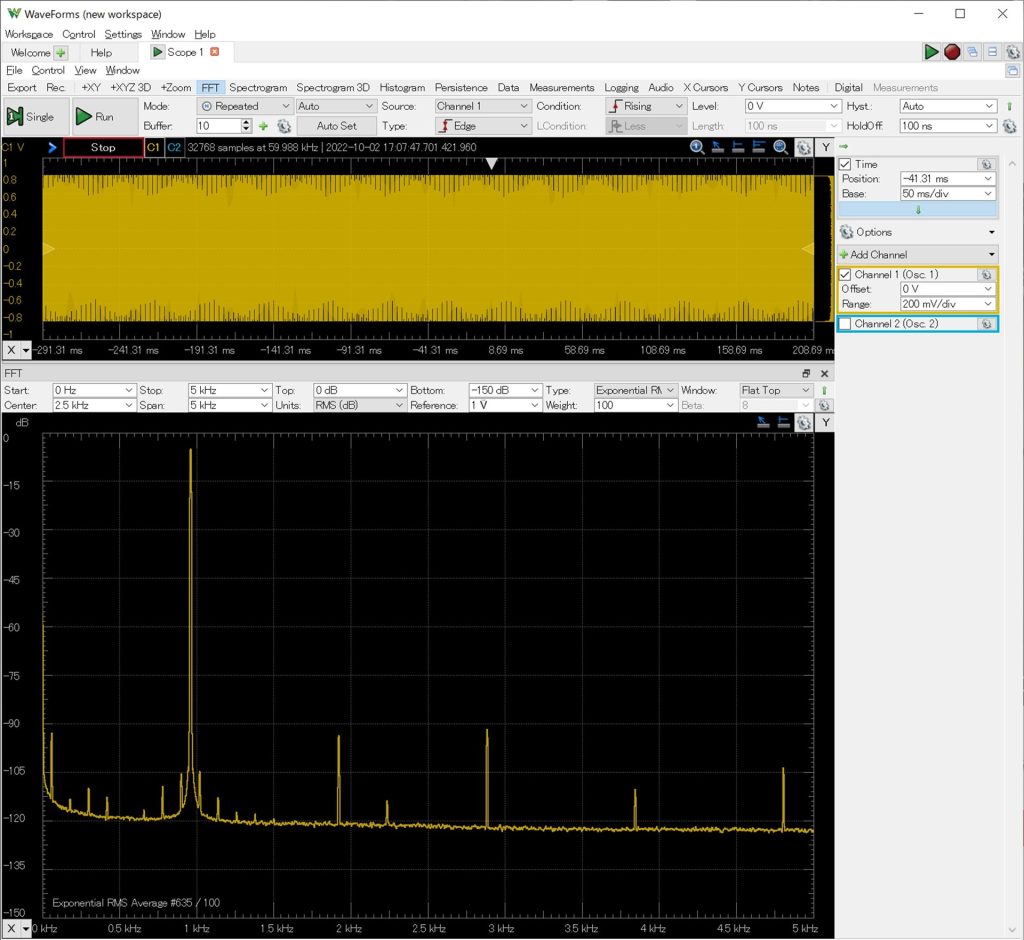
2次~5次高調波が-90[dB]以下になっていることがわかります。ただ、発振周波数付近に小さなピークがいくつも出ているのが気になります。振幅制御回路の制御ループが僅かながら発振しているようです。補償器の積分コンデンサの値を1.5[uF]から10[uF]に変更することで以下のような出力を得ました。しかし、この変更を行うと振幅の収束に時間がかかるためもう少し定数を最適化していく必要があると思いますが、ひとまず傾向がわかったので良しとします。
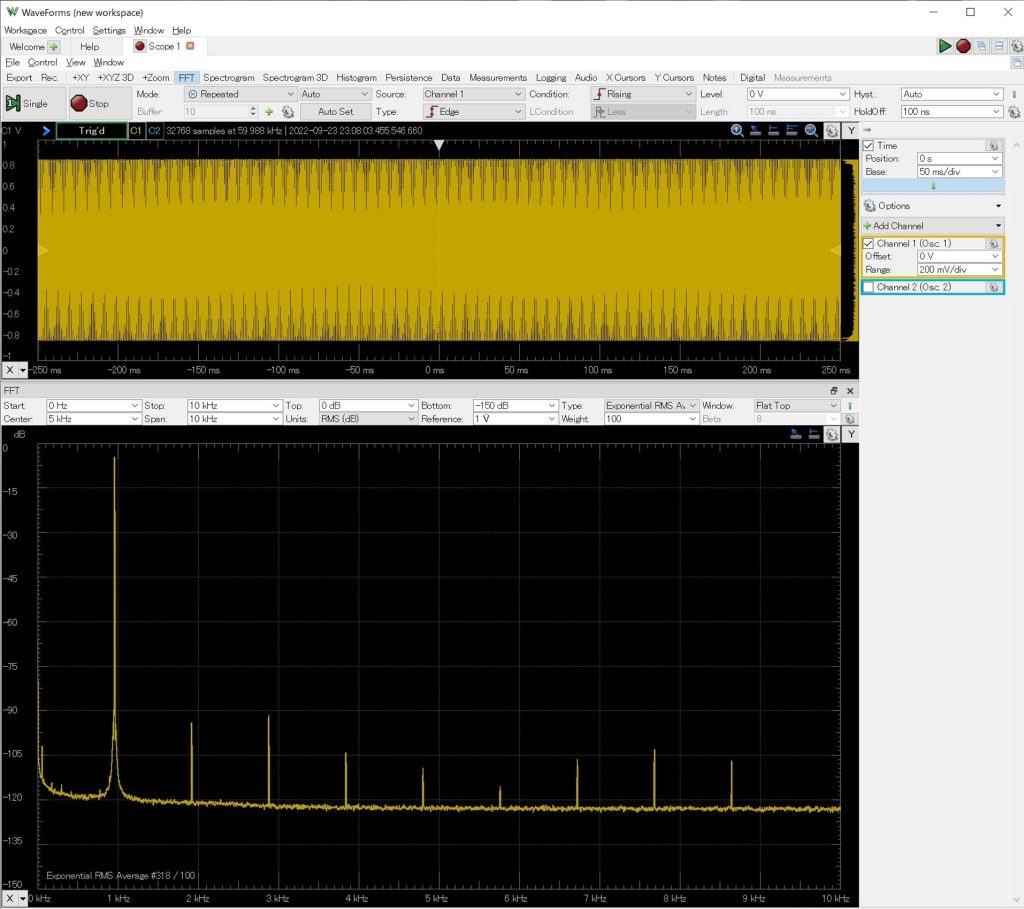
ファンクションジェネレータAFG310の出力を同じ条件でFFT解析した結果を以下に示します。状態変数型の発振回路と比較して2次~5次高調波のレベルが大きいことがわかります。今回製作した状態変数型の発振回路で目的としていた低歪な正弦波を得られているようです。
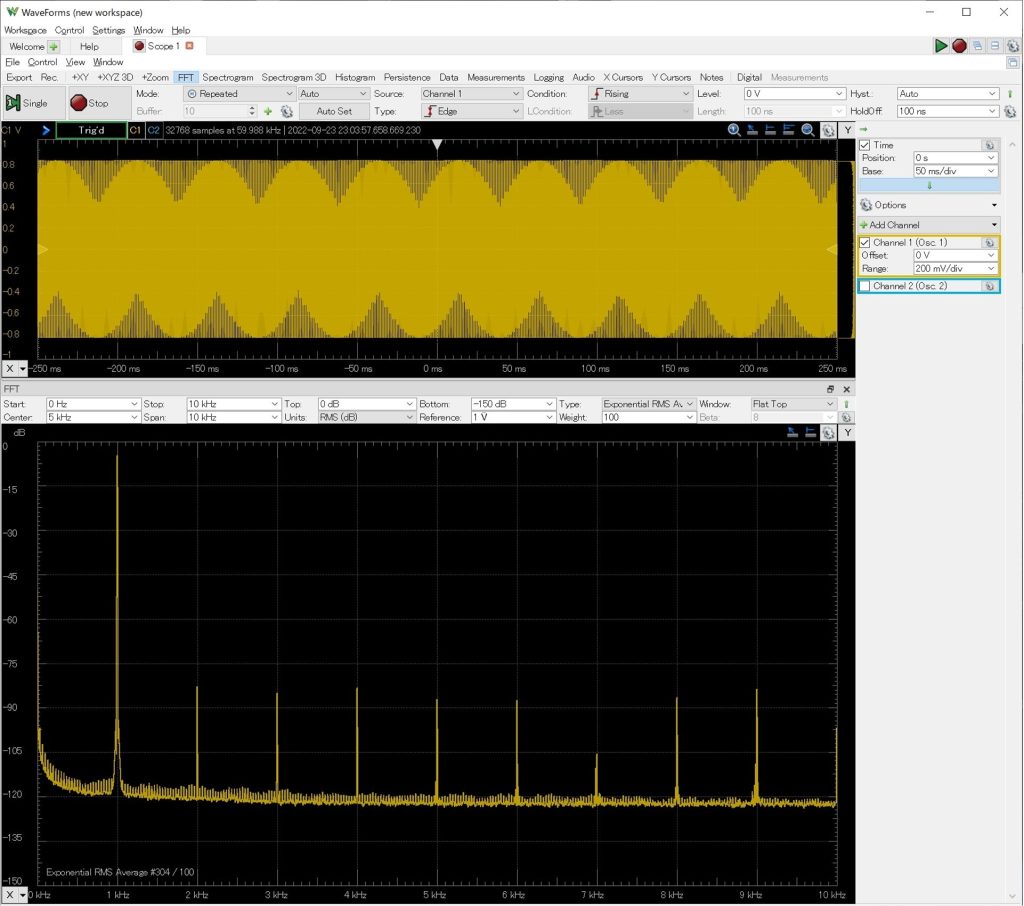
ADP3250(14bitADC)では分解能が不足しているのではないかと考えています。もう少し分解能が高い測定装置を構築して高調波成分の分析を行いたいところですが、丁度良い設備を持ち合わせていません。帯域除去フィルタを作成するか、ラズピコにダイナミックレンジが広く高速なADCを接続して簡易的なデジタイザのようなものを作るのが良さそうです。
参考資料
◆トランジスタ技術 2003年 7月号
◆発振回路の完全マスター
◆図解 アナログICのすべて



コメント