CVCC電源装置の製作 (ソフトウェア、補償器設計)

20V、5A程度の可変電源がほしくなったので製作してみました。スイッチング方式としたので非常に小さく作ることができました。内部構造実験中の電源回路 ■仕様定電圧出力 DC 0~20Vボリュームにより連続可変定電流出力 DC 0~5A

CVCC電源装置のソフトウェア構成について説明します。ハードウェアの記事の続きになります。

CVCC電源装置を製作しました。今回はこのハードウェア構成について詳しく説明します。ブロック図この電源装置はスイッチング方式で出力電圧を安定化させています。スイッチング方式とすることで小型形状で可変出力が可能な電源装置を実現しています。

ソフトウェア構成

Mainコアは、主にユーザーインターフェースの制御を行います。7セグLEDのダイナミック点灯制御やフィードバック制御ループへ受け渡す基準電圧・基準電流設定値の処理を行っています。CLAはフィードバック制御演算を行います。基準値とAD変換値から偏差を取得して定電圧・定電流制御を行います。

CLAはFPUを搭載しているので演算に浮動小数点数を用いることができます。FPUは単精度(float)までのサポートです。フィルタの係数が小さな値となる場合に注意が必要です。

タイミングチャート

フィードバック制御ループは各ペリフェラル(PWMやADC)が出力するトリガを元に動作します。このトリガタイミングはソフトウェアである程度自由に変更することができます。今回はPWMタイマを基本として動作するように設定しました。

①　PWMタイマがゼロクリアされる→AD変換トリガ出力
②　AD変換開始
③　AD変換終了→CLA割り込み発生
④　フィードバック演算
⑤　PWMデューティ更新

①～ ⑤までの動作をPWM周期で繰り返し実行します。

AD変換とデューティの演算はPWM1周期以内に終了させる必要があります。

フィードバック制御演算

データフロー

定電圧制御と定電流制御の切り替え

定電流設定値と実際に流れている電流値を比較して補償器へ入力するデータを切り替えます。通常は定電圧制御を行い、電流値が設定値を上回った時に定電流制御を行う仕組みです。

補償器(制御器) の設計

出力電圧・電流を一定に保つために位相補償が必要になります。位相補償については説明すると長くなってしまうので、代わりに下記の書籍を紹介します。

定本OPアンプ回路の設計: 再現性を重視した設計の基礎から応用まで (定本シリーズ)

DCDCコンバータでよく用いられる位相補償器には、Type-2補償器やType-3補償器というものがあります。Type-2補償器はPI制御、Type-3補償器はPID制御に近い特性を持ちます。

フィードバック制御によく用いられているPI制御やPID制御と異なり非常に多くのパラメータを調整する必要がありますが、その分より細かな位相補償が可能となります。

http://www.tij.co.jp/jp/lit/an/jaja222/jaja222.pdf

今回はマイコンによる演算によってフィードバック制御を行います。したがって補償器(制御器)はマイコン内部に演算として実装する必要があります。

Type-2補償器

Type-2補償器は、以下のような周波数特性を持った補償器です。最大で90度までの位相進み補償が可能です。

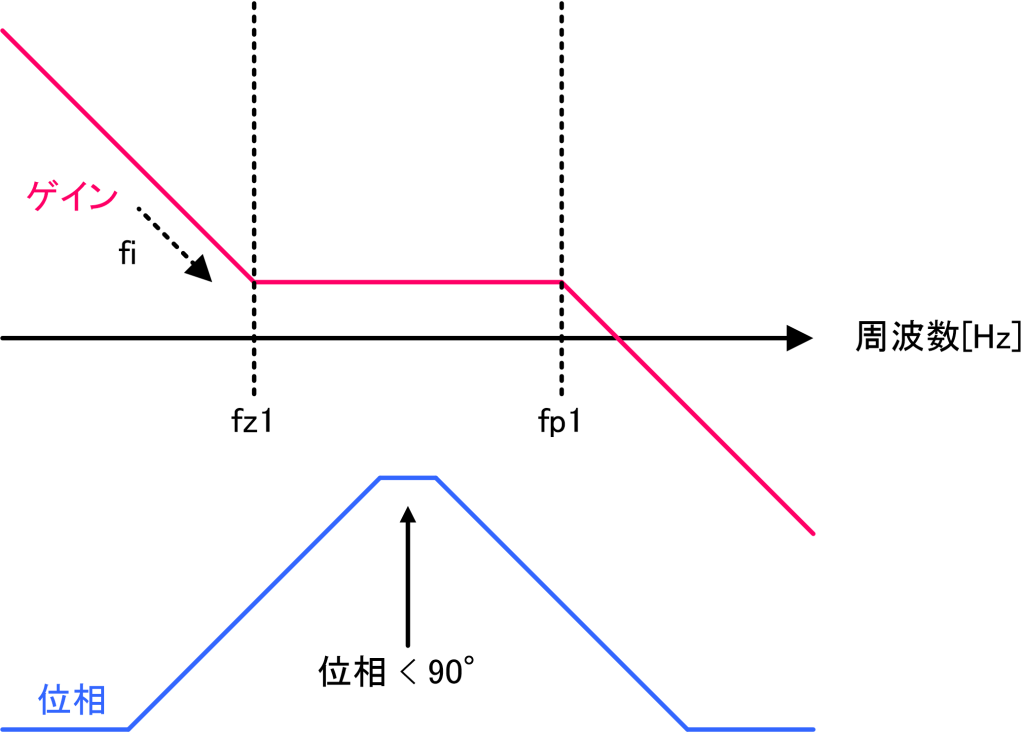
Type-2アナログ補償器

OPアンプを用いて構成したType-2補償器です。アナログ制御方式のDCDCコンバータで一般的に用いられている構成です。アナログ方式のType-2補償器の伝達関数を元にデジタル化された補償器を設計します。

Type-2アナログ補償器の伝達関数

Type-2アナログ補償器の伝達関数は以下の式で表されます。

$$G(s)=\frac{\omega_{i}}{s}\frac{(\frac{s}{\omega_{z1}}+1)}{(\frac{s}{\omega _{p1}}+1)}$$

$\omega_{i}$,$\omega_{p1}$,$\omega_{z1}$はポールとゼロの角周波数[rad/s]です。

$$\omega_{i}=2\pi{f}_{i}$$

$$\omega_{p1}=2\pi{f}_{p1}$$

$$\omega_{z1}=2\pi{f}_{z1}$$

Type-2補償器の離散化

離散化の手法は他の文献で詳しく紹介されているため、ここでは詳しくは説明しません。双一次変換を用いることが多いようです。ちなみにMATLABを用いるとこの変換を簡単に行うことができます。

Type-2補償器は2次のIIRフィルタで特性を再現することができます。

$$H(z)= \frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1-a_{1}z^{-1}-a_{2}z^{-2}}$$

差分方程式は以下のようになります。

$$H(z)=\frac{Y[z]}{X[z]}= \frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1-a_{1}z^{-1}-a_{2}z^{-2}}$$

$$y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]+a_{1}y[n-1]+a_{2}y[n-2]$$

フィルタ係数の算出

IIRフィルタの各係数は以下の式で求めることができます。

$$a_{1} = \frac{4}{2+T_{s}\omega _{p1}}$$

$$a_{2} = \frac{-2+T_{s}\omega_{p1}}{2+T_{s}\omega_{p1}}$$

$$b_{0} = \frac{T_{s}\omega_{i}\omega_{p1}(2+T_{s}\omega_{z1})}{2(2+T_{s}\omega _{p1})\omega_{z1}}$$

$$b_{1} = \frac{(T_{s})^{2}\omega_{i}\omega_{p1}}{2+T_{s}\omega_{p1}}$$

$$b_{2} = \frac{T_{s}\omega_{i}\omega_{p1}(-2+T_{s}\omega_{z1})}{2(2+T_{s}\omega _{p1})\omega_{z1}}$$

$\omega_{i}$,$\omega_{p1}$,$\omega_{z1}$はポールとゼロの角周波数[rad/s]
$T_{s}$はサンプリング周期[s]です。

ブロック図

差分方程式をそのままブロック図に落とし込むと以下のようになります。

一般的に遅延素子数を削減した構成のIIRフィルタが用いられます。入力と出力を入れ替えて遅延素子を共通化できるように配置を変更します。この変更により演算量や記憶領域を節約することができます。

この配置の場合は差分方程式が2つに分けて考えます。入力 $x[n]$の加算点以降を$u[n]$と置いて差分方程式を立てます。この差分方程式をCLA内部の演算として実装します。

$$u[n]=x[n]+a_{1}u[n-1]+a_{2}u[n-2]$$

$$y[n]=b_{0}u[n]+b_{1}u[n-1]+b_{2}u[n-2]$$

Type-3補償器

Type-3補償器は、以下のような周波数特性を持った補償器です。最大で180度までの位相進み補償が可能です。90度以上の位相進み補償を行うことができるのでType-2補償器よりも制御帯域を伸ばすことができます。

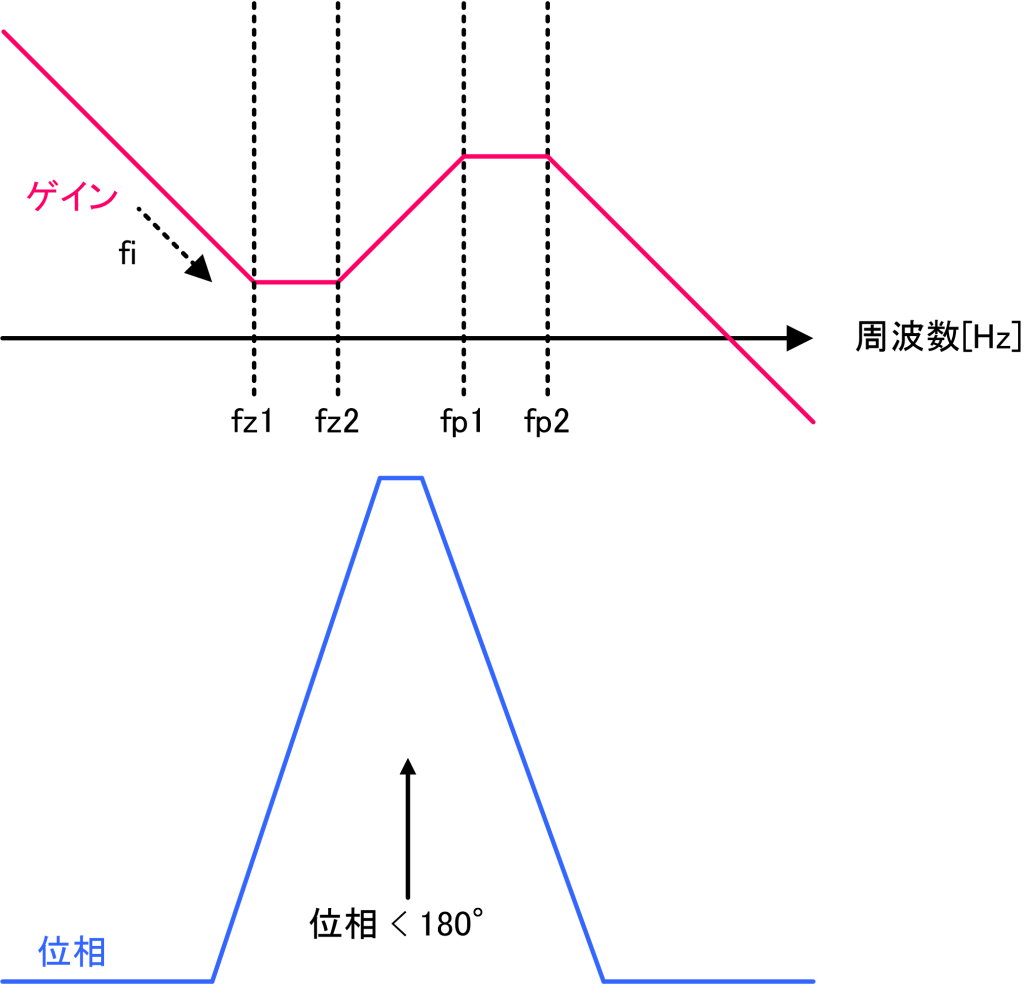
Type-3アナログ補償器

OPアンプを用いて構成したType-3補償器です。Type-2補償器のR1と並列にR3,C2を追加したものです。Type-3補償器と同じようにアナログ方式のType-3補償器の伝達関数を元にデジタル化された補償器を設計します。

Type-3アナログ補償器の伝達関数

Type-3アナログ補償器の伝達関数は以下の式で表されます。

$$G(s)=\frac{\omega_{i}}{s}\frac{(\frac{s}{\omega_{z1}}+1)(\frac{s}{\omega_{z2}}+1)}{(\frac{s}{\omega_{p1}}+1)(\frac{s}{\omega _{p2}}+1)}$$

$\omega_{i}$,$\omega_{p1}$,$\omega_{p2}$,$\omega_{z1}$,$\omega_{z2}$はポールとゼロの角周波数[rad/s]です。

$$\omega_{i}=2\pi{f}_{i}$$

$$\omega_{p1}=2\pi{f}_{p1}$$

$$\omega_{p2}=2\pi{f}_{p2}$$

$$\omega_{z1}=2\pi{f}_{z1}$$

$$\omega_{z2}=2\pi{f}_{z2}$$

Type-3補償器の離散化

Type-3補償器は3次のIIRフィルタで特性を再現することができます。

$$H(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}+b_{3}z^{-3}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}}$$

差分方程式は以下のようになります。

$$H(z)=\frac{Y[z]}{X[z]}=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}+b_{3}z^{-3}}{1-a_{1}z^{-1}-a_{2}z^{-2}-a_{3}z^{-3}}$$

$$y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]+b_{3}x[n-3]+a_{1}y[n-1]+a_{2}y[n-2]+a_{3}y[n-3] $$

係数の算出

$$a_{1}=-\frac{-12+(T_{s})^{2}\omega_{p1}\omega_{p2}-2T_{s}(\omega_{p1}+ \omega_{p2})}{(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})}$$

$$a_{2}=\frac{-12+(T_{s})^{2} \omega_{p1}\omega_{p2}+2T_{s}(\omega_{p1}+\omega_{p2} )}{(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})}$$

$$a_{3}= \frac{(-2+T_{s}\omega_{p1})(-2+T_{s}\omega_{p2})}{(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})}$$

$$b_{0}=\frac{T_{s}\omega_{i}\omega_{p1}\omega_{p2}(2+T_{s}\omega_{z1})(2+T_{s}\omega_{z2})}{2(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})\omega_{z1}\omega _{z2}}$$

$$b_{1}=\frac{T_{s} \omega_{i}\omega_{p1}\omega_{p2}(-4+3(T_{s})^{2}\omega_{z1}\omega_{z2}+2T_{s}(\omega_{z1}+\omega_{z2}))}{2(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})\omega_{z1}\omega_{z2}}$$

$$b_{2}=\frac{T_{s} \omega_{i}\omega_{p1}\omega_{p2}(-4+3(T_{s})^{2}\omega_{z1}\omega_{z2}-2T_{s}(\omega_{z1}+\omega_{z2}))}{2(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})\omega_{z1}\omega_{z2}}$$

$$b_{3}=\frac{T_{s} \omega_{i}\omega_{p1}\omega_{p2}(-2+T_{s}\omega_{z1})(-2+T_{s}\omega_{z2})}{2(2+T_{s}\omega_{p1})(2+T_{s}\omega_{p2})\omega_{z1}\omega _{z2}}$$

$\omega_{i}$,$\omega_{p1}$,$\omega_{p2}$,$\omega_{z1}$,$\omega_{z2}$はポールとゼロの角周波数[rad/s]
$T_{s}$はサンプリング周期[s]です。

ブロック図

差分方程式をそのままブロック図に落とし込むと以下のようになります。

Type-2補償器と同じように遅延素子を削減

入力 $x[n]$の加算点以降を$u[n]$と置いて差分方程式を立てます。Type-2補償器と同じように、この差分方程式をCLA内部の演算として実装します。

$$u[n]=x[n]+a_{1}u[n-1]+a_{2}u[n-2]+a_{3}u[n-3]$$

$$y[n]=b_{0}u[n]+b_{1}u[n-1]+b_{2}u[n-2]+b_{3}u[n-3]$$

制御対象との組み合わせ

補償器と制御対象を組み合わせて定電圧制御のためのフィードバック系を構築してみます。
特性の確認にはMATLAB(Home)を用いました。

MATLAB Home

MATLAB Home で自分の世界を解析および設計。

また、補償器前段のDCゲインは0.001とします。このゲインは全体のゲインスケールを調整するためのものです。

Type-2補償器で制御してみる

Type-2補償器の周波数特性設計

制御対象の周波数特性に合わせてゼロとポール周波数を決定します。
${f}_{i}=$ 700[Hz]
${f}_{p1}=$ 30[kHz]
${f}_{z1}=$ 1.6[kHz]

係数は以下のようになります。
${a}_{1}=$ 1.029612798684
${a}_{2}=$ -0.029612798684
${b}_{0}=$ 0.222942164848
${b}_{1}=$ 0.021339929120
${b}_{2}=$ -0.201602235728

Type-2補償器単体の周波数特性

制御対象と組み合わせた場合の周波数特性

位相余裕=54.2[°]
ゲイン余裕=22.7[dB]
となって安定したフィードバック系が構築されました。

Type-3補償器で制御してみる

Type-3補償器の周波数特性設計

制御対象の周波数特性に合わせてゼロとポール周波数を決定します。
${f}_{i}=$ 700[Hz]
${f}_{p1}=$ 20[kHz]
${f}_{p2}=$ 30[kHz]
${f}_{z1}=$ 1.5[kHz]
${f}_{z2}=$ 3.0[kHz]

係数は以下のようになります。
${a}_{1}=$ 1.257873708494
${a}_{2}=$ -0.264633152863
${a}_{3}=$ 0.006759444370
${b}_{0}=$ 1.062196736738
${b}_{1}=$ -0.783617871698
${b}_{2}=$ -1.045727879254
${b}_{3}=$ 0.800086729181